XOR運算與編碼

程式語言用來開發程式，程式用來處理和解決問題，無論使用C++或C#或Java等程式語言，程式設計的邏輯基本上是相通的。

假設要處理網路世界的安全性問題，首先，無論透過手機或電腦連接網路，每位使用者均以帳號密碼來確認自己獨一無二的身分，進而存取屬於個人的網路資源。為了安全考量，使用者輸入的帳號密碼，不能以原始的格式(明碼)儲存，而需以某種編碼後的結果存放在雲端空間，以降低駭客入侵雲端能直接取得使用者的帳密(明碼)的風險。

C++除了具備加減乘除的運算能力，還具備邏輯運算能力。邏輯運算的四個基本運算子為
& and
| or 
^ xor
!  not

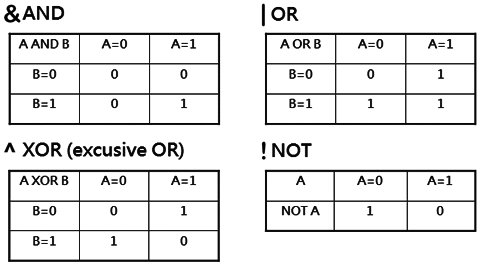
電腦使用二進位數字系統，二進位只有 0 與 1，所以邏輯運算對電腦非常重要，0 與 1 的邏輯運算可以用真值表來表示

對 AND 運算來說，唯有 x y 均為 1 時，x AND y 才為"真"
對 OR 運算來說，只要 x 或 y 有一個為 1，x OR y 即為"真"
對 XOR 運算來說，當 x 和 y 不同時，x XOR y 才得到"真"
而 NOT 就和負號一樣，NOT 0 = 1，NOT 1 = 0

其中 XOR 運算具有可還原的特性，可以應用在編碼運算!

例如，以某個二進位數 10 來說，當它與另一數進行 xor 運算，例如與 11

10 XOR 11 = 01 ( 第一位 1 xor 1 = 0，第二位 0 xor 1 = 1)

用 01 這個結果，再和 11 進行 xor 運算一次

01 XOR 11 = 10 ( 第一位 0 xor 1 = 1，第二位 1 xor 1 = 0)

某數 a 與另一數 b 進行 xor 運算所產生的 c，雖然看起來和 a 不同，但只要以 c 再和 b 進行 一次 xor 運算，就可以重新得到 a，這就是最簡單的可還原編碼的一種方式，b 就是還原的 key！

#include <iostream>

class encoding
{
private:
int key[10]={ 8, 5, 2, 1, 4, 7, 6, 9, 0, 3 }; 

public:
void enc(int x[], int n) {
     for(int i=0; i<n; i++)
x[i] = x[i] ^ key[i];
}

void dec(int x[], int n) {
     for(int i=0; i<n; i++)
x[i] = x[i] ^ key[i];
}

void print(int x[], int n) {
     for(int i=0; i<n; i++)
std::cout << x[i]; 
     std::cout << std::endl; 
}
};

int main()
{
    int mypass[] = { 1, 3, 9, 4 };
    encoding myenc;

    myenc.enc( mypass, 4 );
    std::cout << "編碼結果:";
    myenc.print( mypass, 4 );

    myenc.dec( mypass, 4 );
    std::cout << "解碼:";
    myenc.print( mypass, 4 );

    return 0;
}

在 class encoding 中，enc() 函式與 dec() 函式完全相同，所以就算主程式的解碼部份改呼叫 enc() 函式，當然還是會得到正確的結果。事實上 XOR 運算在磁碟陣列的容錯設計上廣泛被採用，相當有實用價值。

排列組合

排列組合就是一組數字或文字，其中元素依排列位置的不同，而產生的組合。

例如若有一組數列 1、2、3，若增加一個 5，在不改變 1、2、3 順序的情況下，5 可以放在前面、中間或後面，所以可能產生 5 1 2 3，1 5 2 3，1 2 5 3，1 2 3 5 四種組合，也就是在特定 n 個元素排列的條件下，每增加一元素，就會產生 n+1 種新的排列組合。

#include <iostream>

void Permutations(int *list, int n, int x)
{
    for(int i=0; i<= n; i++) //因為多一個元素，所以執行n+1次 
    {
      for(int j=0; j<n; j++) //只列出原始list，多的由 if 處理 
      {
            if(j==i)
                 std::cout << x << " "; 
            std::cout << list[j] << " "; 
      }
      if(i==n) //最後一次 
         std::cout << x;

      std::cout << std::endl;     
    } 
} 

int main()
{
int list[] = { };
Permutations(list, 0, 100);

int list1[] = { 1 };
Permutations(list1, 1, 200);

int list2[] = { 1,2 };
Permutations(list2, 2, 300);
    
int list3[] = { 1,2,3 };
Permutations(list3, 3, 400);

return 0;

}

執行結果

數列 (1) 的排列組合只有 1 種 {1}，而數列 (1 2) 的排列組合，就等於把 2 插入數列 (1 ) ，而得到 {1 2} 和 {2 1}。若對數列 (1 2) 的每種排列組合再增加一個 3，就得到 {3 1 2} {1 3 2} {1 2 3} 及 {3 2 1} {2 3 1} {2 1 3}，即為3個元素的全排列，其項數為 3*2*1=6，4個元素的項數為 4*3*2*1=24... 故 n 個元素的全排列，其項數為 n! 個。

以大風吹的方式看 {1 2 3}，以 1 分別與 2、3 交換位置，可以得到 {2 1 3} 和 {3 2 1} 這兩種排列結果，接著再把{2 3} 交換位置得到 {1 3 2}，同理由 {2 1 3} 和 {3 2 1} 又可得到 {2 3 1} 和 {3 1 2}。

所以全排列就是從第一個元素起，每個元素分別與後面的元素交換位置，適合以遞迴的方式撰寫程式

#include<iostream>

template <typename T>

void swap(T& a, T& b)

{

  T c(a);

  a=b;

  b=c;

}

template <typename T>

void perm(T* list,int start,int length)

{

if(start == length-1)

{

for(int i=0; i<length; i++)

std::cout << list[i] << " ";

std::cout << std::endl;

}

else

{

for(int i=start; i<length; i++)

{

swap(list[start],list[i]); 

perm(list,start+1,length);

swap(list[start],list[i]); 

}

}

}

int main()

{

    int list[] = {1,2,3,4};

    perm(list,0,4);

    return 0;

}

在某些不同的情況，{1 2 3} 需要展開成 {1} {2} {3} {1 2} {1 3} {2 3} {1 2 3} 等項目，例如在檢視購物清單，希望統計 1 2 3 三樣產品的購買記錄和相關性時。

上述需求為描述此 3 個元素 "有" 和 "無" 的組合，而 2 進位就是以 0 與 1 來呈現每一位數的值，故可以藉由 2 進位的對應 000 001 010 011 100 101 110 111 來展開項目組合

#include<iostream>

int pow2(int n)

{

    int r=1;

    while(n-- > 0)

        r*=2;

    return r;

}

template <typename T>

void spreadout(T* list, int len)

{

    int items=pow2(len)-1;

    T newlist[items][len];

    

    for(int i=0; i<items; i++)

    {

        int pos=0, idx=0;

        int binary=i+1;

        while(binary)

        {

            if(binary & 1)

                newlist[i][idx++]=list[pos];

            binary=binary/2;

            pos++;

        }

        

        for(int j=0; j<idx; j++)

        std::cout << newlist[i][j] << " ";

        std::cout << std::endl;

    }

}

int main()

{

    int list[] = {1,2,3,4};

    spreadout(list,4);

    return 0;

}

執行結果

參數的傳遞

C 語言在函數間傳遞參數，有 call by value、call by pointer 兩種方式，而 C++ 則多了 call by reference。以下舉例說明這三種方式的差異。

1.call by value - 參數以值傳遞，函式可以存取參數，但不會改變主程式的變數內容。下面的 test() 函式，將於自動產生 int x = a; 之後才進入函式，所以無論test() 中的 x 值如何改變，都不會影響主程式的 a，即使主程式把 int a 改名為 int x，兩者仍是各自獨立的

void test(int x) { 
    x=100; 

}

int main() { 
    int a = 5;
    test(a);
}

2.call by pointer - 參數以變數的"位址值"傳遞(事實上還是傳值)，函式可以存取指標參數，不會改變叫用程式的指標本身，但透過*存取指標所指向的空間，可改變指向空間的內容。

test1() 於自動產生 int* y = a; 之後進入函式，接著宣告了一個名為 newptr 的 int 指標，然後把參數 y 指標的內容設為 newptr，但返回主程式之後，a 指標的位址並不受影響，*a 的值仍指向 5 而非 100。call by pointer 其實仍是以值的方式來傳遞，只是傳的是個位址值(指標)

#include <iostream>
using namespace std;

void test1(int* y) {
    int* newptr=new int(100);
    y = newptr;
    cout << y << ":" << *y << endl;
}

int main() { 
    int* a=new int(5);
    test1(a);
    cout << a << ":" << *a << endl;
    return 0; 
}

而 test2() 於自動產生 int* y = a; 之後進入函式，此時 *y 與 *a 是指向同一位置，所以執行 *y=50; 就等於改變了 *a，而 y=NULL 則對 a 並無影響

#include <iostream>
using namespace std;

void test2(int* y) {
    *y=50;
    y=NULL;
}

int main() { 
    int* a=new int(5);
    test2(a);
    cout << a << ":" << *a << endl;
    return 0;
}

這也是 call by pointer 又被稱為 call by address 的原因，在還沒有 reference 之前，函式都是使用此方式來修改"指標參數所指向的內容"。

3.call by reference - reference 的符號是 &，此方式直接把主程式的變數交給函式使用，中間沒有隱含自動產生 int x = a; 或 int* y = a; 這類的步驟。以 call by reference 傳遞的參數，若無 const 修飾，函式中對參數內容的任何改變，就等於直接在改變主程式所對應的變數內容

#include <iostream>
using namespace std;

void test3(int (&x)[3], int& y) { //(&x)必需括號，因為[]比&優先權高 
    x[0]=4;
    x[1]=5;
    x[2]=6;
    y=0; 
}

int main() { 
    int a[] = {1,2,3}; 
    int b=100;

    test3(a,b);

    cout << a[0] << " " << a[1] << " " << a[2] << endl;
    cout << b << endl;
    return 0; 
}

由於 call by reference 傳遞快速(尤其是在傳遞物件時)，函式中的程式碼亦比較簡明，所以常被程式設計師採用，若要保持 call by value 的安全性避免函式更動到主程式的變數內容，可在參數前加上 const 常數修飾字即可。

Constructor & Destructor

constructor(建構函式) 與 destructor(解構函式) 是 class 中的兩種特別函式，當主程式中產生某class的物件時，該 class 的建構函式即會自動執行；而當物件生命周期結束，則在物件消滅前會自動執行解構函式。

建構函式和 class 同名，可以有參數，沒有傳回值。解構函式則是 class 名稱前加~符號，沒有參數，也沒有傳回值。由於物件產生時可能會給予不同的參數，所以每一 class 的建構函式可以有很多個，以對應不同的參數。而解構函式因為沒有參數，所以只有一個。

如果程式設計者沒有為 class 撰寫建構函式或解構函式，則編譯器會產生內定的建構函式和解構函式。以下程式可觀察建構函式與解構函式的執行狀況

#include<iostream>
using namespace std;

class myClass
{
public:
   int d[10];
   myClass() {
      cout << "建構函式!" << endl;
   }

   ~myClass() {
      cout << "解構函式!" << endl;
   }
};

void print(myClass x)
{
    for(int i=0; i<10; i++)
        cout << x.d[i] << " ";
    cout << endl;
}

int main()
{
    myClass obj1; //產生物件，應執行 constructor

    print(obj1);

    for(int i=0; i<10; i++)
        obj1.d[i]=i;

    myClass obj2=obj1; //產生物件，應執行 constructor
    print(obj2);
    
    return 0; //obj1 與 obj2 生命週期結束，應執行 destructor
}

程式一開始以 using namespace std; 來表明將使用 std 名稱空間，因 C++ 的標準函式庫都定義在 std 名稱空間，若不宣告使用 namespace std，則當程式使用到 cin cout 這些物件時必須在前加上 std:: 以註明其所在之名稱空間。

這個程式很簡單，主程式先宣告一個 myClass 物件 obj1，接著呼叫 print 函式，把 obj1 裡的陣列印出來。之後再用一個迴圈把數值填入 obj1 裡的陣列，然後再宣告一個 obj2 物件，且把 obj1 的內容做為 obj2 的初始值。最後程式呼叫 print 函式把 obj2 裡的陣列印出來，結束程式。

因為程式中產生了 obj1 obj2 這兩個 myClass 物件，所以 myClass 的建構函式和解構函式都應分別被 invoked 兩次。然而程式執行結果令人驚訝，建構函式只執行一次，而解構函式竟執行了四次！

先前曾提到"由於物件產生時可能會給予不同的參數，所以每一class的建構函式可以有很多個，以對應不同的參數。而解構函式因為沒有參數，所以只有一個"，所以對於上面的執行結果，解構函式被執行四次是正確的次數。而建構函式，因 myClass 中只撰寫了一個無參數的建構函式，若 myClass 物件以【有參數】的方式產生時，就會改去執行編譯器自動產生的建構函式，而不是執行 myClass() 這個無參數的建構函式。

myclass obj2=obj1; //以複製方式產生物件，會執行 copy constructor

這就是少了一次"建構函式!"的原因，但多兩次"解構函式!"又是什麼造成的？
為了釐清這個問題，以下把 copy 建構函式添加到 myClass 中，再觀察執行結果

class myClass
{
public:
   int d[10];

   myClass() {
      cout << "建構函式!" << endl;
   }

   myClass(myClass& obj) {
      cout << "COPY Constructor!" << endl;
   }

   ~myClass() {
      cout << "解構函式!" << endl;
   }
};

執行結果似乎更奇怪了，雖然次數有對應，建構函式被執行了四次(其中有三次是執行 copy constructor)，而解構函式也被執行了四次。但程式裡明明只有兩個 myClass 物件啊！(又是明明惹的禍)

這是因為 void print(myClass x) 函式的參數型態是 myClass 物件，而且以傳值 (call by value) 的方式傳遞。一個物件的【值】如何產生？ C++ 的做法是，自動宣告一個同型態的臨時物件並把主程式的物件參數 copy 過來，再交給函式使用。所以在處理 print(obj1); 時，等於先執行 myClass x=obj1; 然後 print 函式才去印出 x 物件的內容。當 print 完成，返回主程式時，這個臨時物件 x 的生命周期即告結束。

所以每呼叫一次 print 函式一次，就會以 copy 的方式產生臨時的 myClass 物件 x，並在函式返回時消滅，於是 myClass 的 copy constructor 與解構函式都會被執行。 

若要避免這個狀況，可以改用 call by reference 的方式來傳遞物件參數，並加上 const 修飾以避免在函式中更動了物件的內容。

void print(const myClass& x)
{
    for(int i=0; i<10; i++)
        cout << x.d[i] << " ";
    cout << endl;
}

Operator Overloading 運算子重載

在前幾篇的程式中，class myData 已初具動態記憶體管理的能力，然而它幾乎是個無用的 class，因為它只有一個公開的 add 函式可供外界把資料添加進去，沒有辦法取出資料。

若要讓它的資料可以被外部程式存取，可以設計一些 get() set() 等函式，不過看起來不夠簡潔；或者把內部的 int *data 改放到 public: 區段，但這樣又失去封裝的精神...

若是能像使用陣列，例如 a[15] 這樣的方式來存取物件內的資料，且存取機制又能在 class 內部作好管控，應該是比較好的方式。C++ 透過 Overloading 來滿足這類的設計需求。


下列 C++ 的運算子都可以 Overloading (重載) 
+ - * / % ^ & ~ ! = < > += -= *= /= ^= &= << >> >= <= == != && ++ -- [] () new delete | ||

在 class 中設計運算子 Overloading 的語法如下

傳回值型態 類別名稱::operator 運算子(參數)

{
  // Overloading程式碼
}

設計重載程式，必須注意"傳回值型態"。在任何的程式設計中，變數可能出現在等號的左邊或右邊，當位於左邊的時候，它代表一個位址，準備存放等號右邊運算式的運算結果(值)；而當變數位於等號右邊的時候，它則要提供一個值。

Overloading 函式只能傳回一種型態，而索引 [] 運算又要滿足上述兩種可能，所以必須透過 reference (& 參考) 方式傳回。

結合 "Class template 類別樣版/模板" 與 Overloading []，class myData 改寫如下

#include <iostream>

template <typename dType>
class myData
{
//私有區段，只有class內部程式可存取
private:
   int _boundary; //陣列空間上限
   
//保護區段，只有class內部程式和繼承的class可存取
protected: 
   int len;  //資料總數 
   dType *data; //用來存放所有輸入資料的記憶空間指標
   dType errdata; 

//公用區段，class內外部程式均可存取
public:
   myData() //建構函式1，當物件產生時會自動執行(無參數) 
   {
      len=0; //資料長度歸0
      _boundary=10; //邊界設為10 
      data=new dType[_boundary]; //配置10個dType記憶空間 
   }
   
   myData(int n) //建構函式2，參數為陣列大小 
   {
      if(n<=0)
     myData(); //忽略錯誤參數，呼叫建構函式1 
      else
      { 
         len=n; //資料長度為n 
         _boundary=n; //邊界亦為n 
         data=new dType[n]; //配置n個dType記憶空間
          }
   }

   ~myData() //解構函式，當物件消滅時會自動執行
   {
      delete [] data; //釋放data記憶空間
   }
   
   dType& operator[](int n)
   {
      if (n>=len || n<0) //索引超過範圍
      { 
         std::cerr << "索引超過範圍:" << n << std::endl;
         return errdata; //回傳一個存在但無用的參考 
      }
      return data[n]; //ok，回傳 data[n] 的 reference 
   }

   void add(dType d)
   {
     if (len>=_boundary-1) //資料滿了，增加記憶空間
     {
       dType *nptr=new dType[_boundary+10]; //多配置10個dType記憶空間
       for(int i=0; i<len; i++)
         nptr[i]=data[i]; //把舊資料複製到新的位置
       delete [] data; //釋放舊的記憶空間
       data=nptr; //資料指標指向新的位置
       _boundary+=10;
     }
     data[len++]=d; //把參數d放在最後的位置後再把資料長度+1
   }
};

int main()
{
   myData<float> d(5); //宣告物件 d 有 5個 float 

   for(int i=0; i<7; i++) //故意超過範圍 
   { 
       d[i]=i/7.0; //d[i]是位址 
       std::cout << i/7.0 << std::endl; 
   }
   
   d.add(100); //再加一個元素到後面
  
   for(int i=0; i<7; i++) //故意超過範圍 
       std::cout << d[i] << std::endl; //d[i]是值  

   return 0;

}

現在以 myData 所宣告出來的物件已經可以如同陣列一樣的使用了，若再加上一些函式，可實現更自由的動態調節大小，以增加程式設計的彈性。

Template與繼承的組合

C++ 中的 Template 大致有三種用法，Function Template、Specialization，和 Class Template。

Function Template 就是保留函式的參數型態，或函式內的變數型態，等到執行時再依主程式傳入的參數來決定，以提高函式的泛用性，例如

#include <iostream>

template <typename T>
void swap(T& a,T& b) {
   T tmp=a;
   a=b;
   b=tmp;
}

template <typename T1, typename T2>
T1 max(T1 x, T2 y)
{
  return (x>y) ? x : y;
}

int main() {
   float x=3.14, y=98.9;
   swap(x,y);
   std::cout << x << " " << y << " " << max(x,99);
   int a=1, b=2;
   swap(a,b);
   std::cout << a << " " << b << " " << max(a,b);
   return 0;
}

上面第一個 swap 函式僅以主程式傳來的一種參數型態運作，所以 a b 參數的型態必須相同，否則會產生編譯錯誤。第二個 max 函式則接受兩種參數型態，T1 與 T2 型態可以相同或不同(不考慮是否影響程式運算)，並以T1參數型態之值回傳。template <typename T>的寫法可改為 template <class T>，兩者功能一樣。

Specialization 特化，就是例外處理，由於 Function Template 讓函式產生泛用性，但若有需要對特定的資料型別進行其他處理，則可宣告一個同名 Template 函式並指定參數型別，來撰寫例外處理程式

#include <iostream>

template <typename T>  //樣板函式1
void swap(T& a,T& b) {
   T tmp=a;
   a=b;
   b=tmp;
}

template <> //樣板函式2
void swap<int>(int& a,int& b) {
a=b=0;
}

int main() {
   float a=50, b=100;
   swap(a,b); //float 叫用樣板函式1
   std::cout << a << " " << b << std::endl;
   int x=50, y=100;   
   swap(x,y); //Specialization, int 叫用樣板函式2 
   std::cout << x << " " << y << std::endl;
   return 0;

}

第三種 Class Template 在 "Class template 類別樣版/模板" 這篇已有介紹，以下針對一般 Class 和 Class Template 之間繼承情況做一整理。

按照一般 class 與 class template 分別為父類別、衍生類別的排列組合有四

父類別	衍生類別
class	class
class	template
template	class
template	template

以上四種組合在 C++ 中都是允許的，以下程式即示範各種繼承關係

#include <iostream>

class baseClass1 {
public:
    int a;
};

template <typename T> class baseClass2 {
public:
    T b;
};

class sonClass1 : public baseClass1 {
public:
int c;
};

class sonClass2 : public baseClass2<float> {
public:
int d;
};

template <typename T> class sonClass3 : public baseClass1 {
public:
T e;
};

template <typename T> class sonClass4 : public baseClass2<int> {
public:
T f;
};

template <typename T> class sonClass5 : public baseClass2<T> {
public:
T g;
};

int main()
{
baseClass1 b1;
baseClass2<float> b2;
sonClass1 s1;
sonClass2 s2;
sonClass3<float> s3;
sonClass4<float> s4;
sonClass5<float> s5;

b1.a=1; //int

b2.b=3.14; //T

s1.a=1; //int
s1.c=1; //int

s2.b=3.14; //T
s2.d=1; //int

s3.a=1; //int
s3.e=3.14; //T

s4.b=3.14; //T int
s4.f=3.14; //T

s5.b=3.14; //T
s5.g=3.14; //T

std::cout << b1.a << std::endl;
std::cout << b2.b << std::endl;
std::cout << s1.a << std::endl;
std::cout << s1.c << std::endl;
std::cout << s2.b << std::endl;
std::cout << s2.d << std::endl;
std::cout << s3.a << std::endl;
std::cout << s3.e << std::endl;
std::cout << s4.b << std::endl;
std::cout << s4.f << std::endl;
std::cout << s5.b << std::endl;
std::cout << s5.g << std::endl;

    return 0;

}